Machine learning for GPP

Machine learning (ML) models are widely used to predict gross primary production (GPP) from ecosystem flux measurements, yet most ignore key temporal dependencies such as thermal acclimation, soil moisture stress, and cold acclimation. These factors influence photosynthesis over time, but many ML models treat GPP observations as independent, potentially limiting their accuracy and generalizability. While process-based models incorporate known physiological mechanisms, they often struggle with flexibility. This project compares a mechanistic photosynthesis model (P-model), a standard ML model (MLP), and a recurrent neural network (LSTM) to assess how well they capture temporal patterns and generalize across ecosystems.

Our results (see figure below) show that both ML models outperform the process-based approach. The LSTM effectively captures seasonal dependencies and generalizes well to moist, seasonal sites. However, errors increase under extreme drought, particularly in evergreen forests where water stress effects are harder to detect. The LSTM performs better than the MLP in arid regions, suggesting that temporal memory enhances GPP predictions in water-limited conditions. However, performance remained highly variable in arid regions.

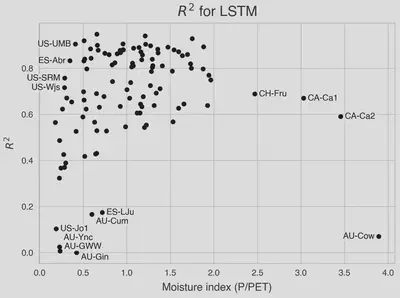
As climate change intensifies water stress, improving GPP models is increasingly important. Our findings highlight the potential of recurrent neural networks for capturing long-term environmental influences but also reveal challenges in arid regions.

Results of this study will be presented at EGU 2025: Session: AS3.44 – Understanding feedbacks between greenhouse gas exchange processes and climate variability using in situ observations, remote sensing, and machine learning